Even in this multi-core era, traditional programming methods don’t take full advantage of multi-core systems. To do that, applications must use threads to execute code in parallel. OpenMP, an API for writing multi-threaded programs in a relatively easy way, can run on a variety of single- and multi-processor systems. It uses the Shared Memory Model, and mainly comprises compiler directives and environment variables used in C, C++ and FORTRAN. It is widely available across various architectures and operating systems. In this article, I will discuss how to use the OpenMP API to speed up an operation.
Let’s cover a few basics about OpenMP before proceeding to our Matrix Multiplication operation. OpenMP is designed keeping in mind the perfect UMA (Uniform Memory Architecture) system, where all memory access latencies are the same. However, a NUMA (Non-Uniform Memory Architecture) system has variable latencies, depending upon the distance and the design topology used. I have used a NUMA system here for benchmarking. Since the detailed discussion of NUMA is beyond the scope of this article, please refer to Wikipedia and other resources.
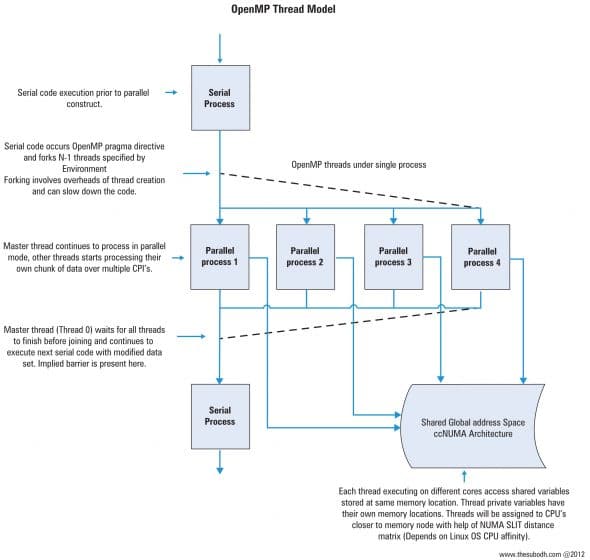
Thread placement can be controlled using various CPU affinity features of the OS, as well as OpenMP. In Linux, NUMA systems threads are placed on CPUs closer to the allocated memory region, to avoid high memory access latencies. This is dynamically controlled by the Linux kernel, unless specified by the user. OpenMP version 4.x will have better support for NUMA systems. Code can contain both serial and parallel statements and all the ugly syntax of threading is hidden behind the OpenMP pragma directives. OpenMP is best for loop-level parallelism, without many critical sections. Threads will be forked according to the pragma directives and joined after completion.
Using OpenMP, we can construct multiple parallel regions within the same code. Multiple threads can be forked on the occurrence of every parallel region construct. Thread creation involves certain overheads, which must be taken into consideration while writing scalable parallel code. OpenMP allows us to fork threads once, and then distribute nested parallel regions on these threads, reducing the overhead of thread creation on every parallel construct. Operations such as flush() help us to maintain data integrity between nested threads. OpenMP usually distributes one thread per core. More threads per core can cause a decrease in performance by stealing CPU time, though this behaviour depends upon the application and system configurations.
Advantages of OpenMP
- Easy to program. More readable code.
- Data layout is handled automatically by OpenMP directives.
- Threads can move from one core to another, unless specifically bound.
- Easy modification of environment settings.
- Guaranteed to perform efficiently on Shared Memory Systems.
- Portable and widely available.
Disadvantages
- Performance may decrease after a finite number of threads, as all threads will compete for shared memory bandwidth. To reduce this, threads must be placed properly closer to CPUs, depending upon the applications requirements.
- Thread synchronisation is expensive.
- Available on SMP (Symmetric Multi-processing) systems only.
- Not as scalable as MPI (Message Passing Interface), although a hybrid model of MPI + OpenMP + OpenMP CUDA is getting a lot of attention.
Parallel matrix multiplication
As part of learning OpenMP, I have written code for Parallel Matrix Multiplication. The algorithm used is a conventional one we all learned in school (see Figure 2). Lots of optimised algorithms exist, but lets leave that for another article.
System/software information
System: SGI Altix UV1000 (128-core 16-CPU Node 1 TB RAM Fat-Tree model cc-NUMA)
- OS: RHEL 6.1 x86_64
- GCC version: Red Hat 4.4.5-6
To reduce the required space, the source code is provided separately. Download it (psmm.c) from https://www.opensourceforu.com/article_source_code/june12/parallel_matrix_code.zip.
Code compilation and output
I compiled the code with GCC optimisation level 2. The sample code output shown below is produced for 128 threads, matrix size 3000 and chunk size 1:
server1 [root]> gcc -O2 omp_mmul_svp.c -o omp_mmul fopenmp server1 [root]> ./omp_mmul 128 3000 1 Multiply Array memory allocation... Assigning array elements with '1' for multiply op... Matrix multiplication with openmp... Chunk Size = 1 Total worker threads invoked = 128 [+]multiply_op_omp_time 4.379983 sec Single thread verification complete...OK
Thread monitoring
To monitor threads on the system, start the top utility with the Threads toggle option enabled, i.e., top H. Threads are part of the same process. Using the P column in top, we can determine the core used for processing the thread.
Code information
Frequently used shared and thread-private variables are initialised as register variables, directing the compiler to keep them in CPU registers for faster access. The number of worker threads to be invoked is provided through the omp_set_num_threads() function. If not specified, OpenMP will invoke one thread for each CPU core in the system. A 2D array is initialised, followed by memory allocation using malloc(). Now we need to analyse the result of matrix multiplication because it could contain erroneous results, due to race conditions, which are common in parallel programming. So I have chosen static data for matrix elements, to verify the results easily using serial code. Here, I have assigned m1 and m2 matrices with ‘1’ as the element value, so that each element in mul matrix would end up as the same value given by the user as per the matrix size. For example, if the matrix size is 3000, then mul[0][0] would be 3000 (if the operation is error-free). Now, assigning values to elements of m1 and m2 will take long, especially if the matrix is large. To circumvent this, I have used a conditional pragma directive here. If the matrix size is over 2000, the for loop will become parallelised. Parallel assignation of values to m1 and m2 improves performance, because the assignment operators are independent of each other. Never use function calls in parallel unless they are parallel too.
The operation time calculated is only for the multiplication section of the code. OpenMP provides the function omp_get_wtime() to report the current time. The difference between the start time and the end time is the time required to perform the parallel multiplication operation.
The parallel region with global shared variables for matrix data and the global private variable for the thread number is followed by a parallel for region. The Pragma for statement applies only to one loop; a nested for loop parallelism is achieved using multiple pragma omp directives. By default, in the pragma for directive, the variable ‘i ‘ will become private because I explicitly declared them as private to make the code more understandable. The default type in pragma omp parallel constructs is shared unless specified; you can change it by using default(private) in the pragma omp parallel statement.
The nowait clause in the pragma for statement will remove the implied barrier at the end of the parallel region, and continue to execute the next statement in the pragma omp parallel region. Threads that complete their jobs early can proceed straight to the next statements in work-sharing constructs, without waiting for other threads to finish. This is typically used if more than one pragma for loop is present in the parallel region. The combination of the schedule clause (work-load distribution) and the nowait clause must be adjusted to optimise the code. The schedule clause divides iteration of pragma for loops into contiguous subsets known as chunks, and distributes them on threads as per the types. These options can be hard-coded, or can be specified in environment settings at run time. Let’s compare two types of schedule clauses, static and dynamic:
- Static: Iterations are equally divided and statically distributed among threads. Chunks are calculated automatically, and assigned to threads in a round-robin fashion, depending on the order of the thread number.
- Static, chunk_size: Iterations are divided into the N chunks specified, and statically distributed among threads. The distribution remains the same as in static mode, except that the chunk size is also specified here.
- Dynamic: Iterations are divided according to the default chunk size (1), and dynamically distributed among threads. Iteration chunks are distributed to threads as they request for them. Threads process a chunk, and then request for a new chunk, until no chunks are remaining. The default chunk_size is 1, so each thread will be given one iteration.
- Dynamic, chunk_size: Iterations are divided into the N chunks specified, and dynamically distributed among threads. The distribution policy remains the same as in dynamic mode, with the only difference being that each thread will be given N iterations to process. Efficient load balancing is achieved using dynamic mode, which also adds processing overhead.
Note: There are more types in the schedule clause (such as guided, auto and runtime) which have not been covered in this article. Refer to the OpenMP API guide for details. Depending on your code, I suggest you use the Gprof profiler to check for unexpected wait states in parallel code.
A performance graph of threads vs chunk size
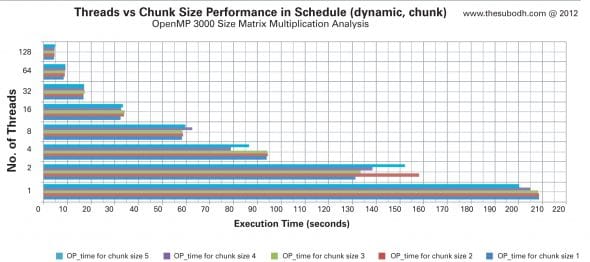
As you can see in the above figure, a single-thread process results in a different execution time for different chunk sizes. It is evident that one thread on a single core will compete for CPU time, hence one time slot performs operations on N loops. A higher chunk size indicates more performance on a single thread, with less overhead of dynamic schedule allocation. The single-thread operation of OpenMP code is slower than plain serial code, due to the overheads involved.

For two-thread operations, a chunk size of 2 takes more time to complete than all other chunk sizes. Chunk size 1 provides maximum performance. For four-thread operations, chunk size 4 yields maximum performance with approximately 188 chunks to be processed by each thread. If we go on increasing the number of threads to the maximum number of cores present in the system, i.e., 128, the performance difference between different chunk sizes vanishes. There is a slight difference between chunk size performances with 128 cores; this is because of the overheads of the dynamic schedule option that requests for chunks to process. In dynamic mode, threads are spawned slowly as each thread requests for chunks of data to process. Since there is a possibility of a job being completed before spawning of all specified threads, it is necessary to choose the chunk size and number of threads wisely if the system is used for multiple parallel programs.
A performance graph: dynamic vs static schedules
This benchmark is performed with no chunk size specified to the schedule clause. For the static type of schedule, the chunk size will be calculated automatically with equal distribution in mind. For the dynamic type, if the chunk size is not specified, it is one so each thread will be provided with one iteration of the for loop to process, and after completion it can request a new iteration to process. In NUMA systems, iterations processed closer to the allocated memory location will complete faster, as compared to distant iteration processing nodes, due to memory access latencies. The static schedule will load all specified threads immediately with calculated chunk sizes. Up to 16 threads, there is a significant difference between the performance of dynamic and static schedules, but after that the difference vanishes. The use of dynamic scheduling increases performance for a lower number of threads.
- OpenMP behaviour is dynamic; you must tune parameters according to the underlying system to get the best performance.
- Idling threads are of no use at all; try to load threads equally, so that they complete their job at the same time.
- Use OpenMP only when there is sufficient workload.
- Avoid forking/joining of threads at every parallel construct; reuse invoked threads.
- Play with code and observe the performance to obtain the best results.
- Parallel code is very hard to debug, as it silently produces wrong results. Verification is mandatory for error-free parallel code.