SageMath is powerful open source software for scientific computing, and it is important to get familiar with it in these days of AI-based applications. The first part of this series on SageMath will introduce you to its installation and basic usage.
Numerous choices abound if you are interested in learning an advanced computing tool, supplementing your already rich repertoire of traditional and popular programming languages and tools. Nevertheless, I propose an outstanding recommendation for your consideration: SageMath. SageMath is a computer algebra system (CAS) with utilities that span nearly all fields of mathematics. It is free and open source software licensed under GNU GPL. SageMath is very powerful software and an open source alternative to proprietary scientific computing tools like Maple, Mathematica, MATLAB, etc. The initial development of SageMath was undertaken by William Stein, and the inaugural version was released in February 2005. Figure 1 illustrates the SageMath logo.

But let us first address a significant question: Why should students or professionals in the field of computer science consider learning scientific computing software? Is mastering conventional and widely-used programming languages like Python, Java, C++, C, JavaScript, etc, not enough? Well, we must explore software like SageMath due to the dynamic nature of our times. The emergence of AI-driven applications compels us to move beyond traditional programming and conventional software. Today’s end users seek software that leverages AI and machine learning techniques, necessitating a strong foundation in scientific computing. In such contexts, software like SageMath becomes indispensable and highly valuable.
Another crucial question is: what sets SageMath apart when there are numerous CAS software and scientific computing tools such as GAP, Maxima, and Singular, as well as Python scientific computing libraries like NumPy, SciPy, among others, readily available? SageMath consolidates numerous specialised CAS software packages into a unified interface that closely resembles Python. As a result, prospective users only need to be familiar with Python syntax, rather than mastering the unique conventions of multiple CAS software systems. Apart from offering this unified interface, SageMath also has several exclusive functions and utilities.
If you are convinced that investing time in learning SageMath is worthwhile, note that while it is easy to start using SageMath, mastering it may take some time. Therefore, I will present a series of articles to cover key topics in the vast realm of SageMath. The series will commence with the installation and basic usage of SageMath, accompanied by simple examples. Subsequently, it will delve into functions associated with various fields of mathematics, including but not limited to graph theory, combinatorics, numerical analysis, number theory, statistics, algebra, linear algebra, calculus, and more. You may be wondering about the relevance of delving into these challenging mathematical topics. However, it’s crucial to note that these mathematical concepts serve as the foundation for scientific computing, which, in turn, represents the future of computing. The series aims to discuss the fundamental mathematical theories required, followed by extensive coding examples.
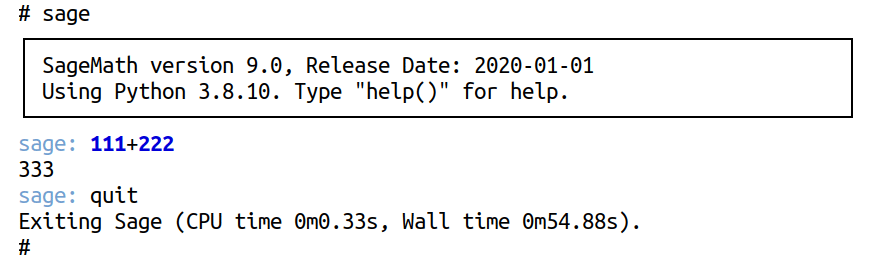
Now, let us learn how to use SageMath on your system. We will explore three different methods, and you can choose the one you prefer. First, you can install SageMath locally on your system. Local installation of SageMath is straightforward, especially on Linux. For instance, in Ubuntu, the command ‘sudo apt install sagemath’ will install SageMath. Alternatively, you can use Ubuntu Software Center or GNOME software to install SageMath directly. To open the SageMath interactive shell, execute the command ‘sage’ in the terminal. This command initiates the SageMath shell, which is essentially a modified version of the IPython shell. Figure 2 shows the interactive shell of SageMath. Notice that I have SageMath version 9.0 installed in my system. In Figure 2, you can also observe a simple addition being carried out. Note that the command ‘quit’ closes the SageMath shell.
The second method is to use JupyterLab, a powerful web-based interactive development environment. JupyterLab is free and open source software, and if you are not familiar with it, it may be a good idea to explore its capabilities. JupyterLab can be installed locally using the command ‘pip3 install jupyterlab’. The command ‘jupyter-lab’ will launch JupyterLab in the default web browser of your system. Since you have already installed SageMath on your system, JupyterLab will automatically detect the SageMath kernel. In Figure 3, you can see the JupyterLab window, where you can select the desired programming language kernel. As I am using Python, Julia, and SageMath from JupyterLab, Figure 3 displays three kernel icons for selection. Please note that this may vary on your system. Clicking on the SageMath kernel icon (highlighted with a red box) opens a Jupyter Notebook window. These windows feature cells that can contain executable code as well as text. Notice that the extension of a Jupyter Notebook file is ‘.ipynb’.

I have previously mentioned that the basic syntax of SageMath is similar to Python. Now, let us run our first simple SageMath code to test this statement. We will execute the following two lines of code in the Jupyter Notebook cell: ‘print “Hello World”’ (Python 2) and ‘print(“Hello World”)’ (Python 3). Figure 4 displays the Jupyter Notebook window with the output after executing the above mentioned lines of code. What observations can you make from Figure 4? Well, the Python 2 version of the code results in a syntax error, whereas the Python 3 version executes correctly. Therefore, when writing SageMath code, please remember to consistently use Python 3 syntax, as there are subtle differences between the two versions of Python.

Now, we will discuss the third and easiest method to execute SageMath code from your system. We will use a web-based cloud computing platform called CoCalc, which directly supports SageMath worksheets. These worksheets can interactively evaluate SageMath code. The extension for CoCalc Notebooks is ‘.sagews’. An important aspect of CoCalc is that it operates on a freemium model where you have to pay for certain services. However, I have found the unpaid version of CoCalc powerful enough for most requirements. Though not free (as in free beer), CoCalc is open source software hosted by SageMath Inc. The developer of CoCalc is also William Stein, the initial developer of SageMath. CoCalc is available online at ‘https://cocalc.com/features/sage?utm_source=sagemath.org&utm_medium=icon’. Additionally, the home page of SageMath, available at ‘https://www.sagemath.org’, has a link to the CoCalc platform.
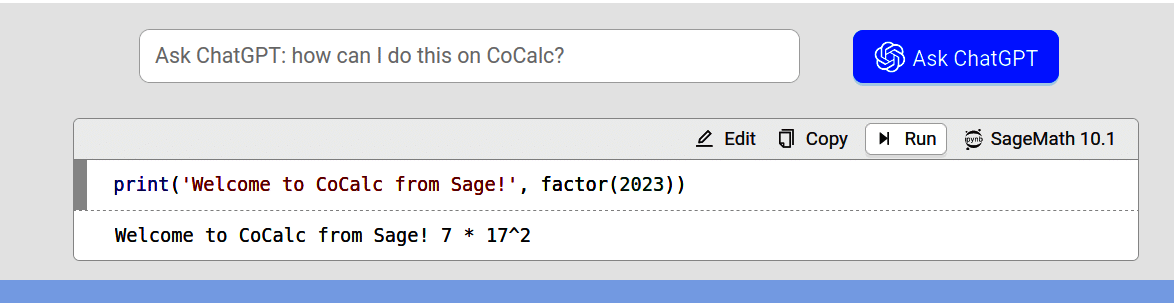
In the first few articles in this series, we will be using CoCalc, as new users can immediately start using SageMath without any installation. You don’t even need to register to execute SageMath code with CoCalc. However, if you want to save your work for later, you need to register and log in. If you prefer, you can use one of your accounts on GitHub, Google, Facebook, X (Twitter), etc, to log into CoCalc. Figure 5 shows the CoCalc environment (with ChatGPT enabled) available on the home page itself. Notice that CoCalc offers SageMath version 10.01.
Now, log into the CoCalc platform to save your work for the future. Let us proceed to write the SageMath code to find the sum and average of an array of numbers. The code is:
Import numpy as np arr = np.array([2, 4, 5, 4, 5, 5, 3, 6, 11, 7]) s = np.sum(arr) avg = np.mean(arr) print(“Sum:”, s) print(“Average:”, avg)
The first line of code imports the Python library called NumPy. The second line uses the NumPy function array( ) to create an array. The next two lines of code use the NumPy functions sum( ) and mean( ) to find the sum and average, respectively. The last two lines of code print these results. Upon execution in CoCalc, the above code will print the sum as 52 and the average as 5.2.
You may now feel tricked, as I have yet again provided Python code masquerading as SageMath code.
I intentionally did this to highlight the crucial point that SageMath not only employs Python 3 syntax but can also seamlessly utilise Python libraries as if they are native to SageMath. This integration significantly enhances the capabilities of SageMath. However, I still believe that ending our discussion here may give the impression that I am just trying to sell a different version of Python to you. Trust me, that is not my intention. So, let us delve into the true strength of SageMath, which Python cannot replicate, through a straightforward example. Consider the pure SageMath code (not Python code) shown here:
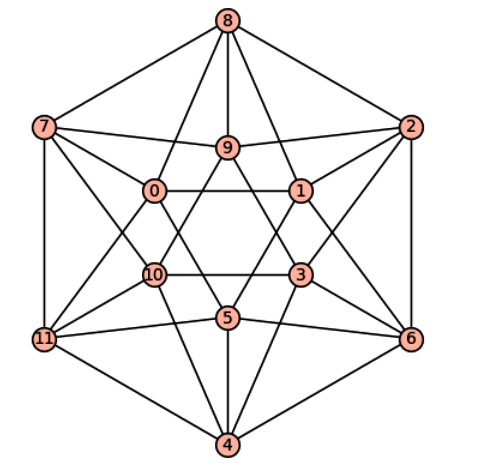
g = graphs.IcosahedralGraph( ) g.show( )
First, let us attempt to understand the meaning of the code. In the first line of code, a variable g is assigned the value of an icosahedral graph created using the function graphs.IcosahedralGraph( ) from SageMath’s graph module. An icosahedral graph is a representation of the vertices and edges of an icosahedron, a Platonic solid. To learn more about icosahedrons and their properties, please refer to the Wikipedia article on Platonic solids. The second line of code calls the method show( ) on the graph object g, which displays the icosahedral graph. Figure 6 illustrates the output of this code.
Now, it is time to conclude our discussion. In the next article in this series, we will discuss graphs, which are mathematical structures used to model pairwise relationships between various objects. But, why do we need to discuss such mathematical structures? In an age marked by widespread social media usage, graphs prove invaluable in capturing relationships between diverse entities such as people and objects. So we will delve into the fundamentals of graph theory—a branch of mathematics/computer science dedicated to studying graphs—and engage in substantial SageMath coding to process graphs.