It’s that time of the year when lists of all kinds are being made. So why not a list of open source tools to be used by mathematicians? The authors of this article have sifted through a number of tools and have come up with a selection that will be of immense use to mathematicians.
Over the past many years, we have gone through a large number of ‘Top Ten’ lists on various topics, both technical and non-technical. Some of them are quite interesting and others boring to the core. For example, ‘The top ten Linux distributions of all time’ is definitely an interesting read, whereas ‘The top ten things to do with a glass of water’ is downright useless, if not boring. Yes, the Internet is full of interesting, boring and stupid Top Ten lists, but we never came across a list enumerating open source tools used by mathematicians—professionals as well as academicians. So, we are listing out the top ten open source tools that are much used by mathematicians.
bc
The utility called bc (basic calculator) is an arbitrary-precision calculator language. This utility is often called the bench calculator and can be invoked with the command bc on a terminal. The two important versions of bc currently used are POSIX bc and GNU bc. GNU bc is available as free and open source software licensed under the GNU General Public License. The decision to include a tool like bc whose development started in 1975 in such a list might be a bit controversial. Of course, there are far more powerful tools available to choose from. Yet, we chose it because, first, it is an arbitrary-precision calculator limited only by the available memory of the host system and not limited to 8, 16, 32 or 64 bits of precision. This, really, is an important thing and if you have any doubts, ask those programmers working in the field of scientific computing, who are plagued by the proper representation of floating-point numbers and how difficult it is to tame them.
Another reason is that though it looks very simple, bc is a Turing complete language, making it as powerful as programming languages like C and Java—at least in theory. The final reason for choosing bc for this list is that you don’t need a gun to kill a fly. On many occasions, it is a case of overkill to use powerful tools like Scilab or SageMath for simple numeric computations. Figure 1 shows the output of a division operation using bc with various levels of precision.
Scilab
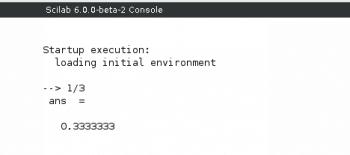
Scilab is an open source, cross-platform numerical computational tool and a numerical programming language licensed under the GNU General Public License. It can be used for signal processing, statistical analysis, image processing, fluid dynamics simulations, numerical optimisation, etc, often with the help of toolboxes like Image Processing Toolbox, Wavelet Toolbox, etc. Scilab is an open source alternative to MATLAB, another very popular but proprietary numerical computing environment. The two tools resemble each other to some extent, so that often a person skilled in one will find it easy to migrate to the other. A comparison of Scilab and MATLAB is clearly out of the scope of this article, but there is at least one area where Scilab clearly outperforms MATLAB, and that is, price! You absolutely don’t have to pay anything to use Scilab, whereas MATLAB is a relatively costly scientific tool. Scilab can be used as a programming environment and an interactive mathematical shell. Figure 2 shows how Scilab works as an interactive mathematical shell.

GNU Octave
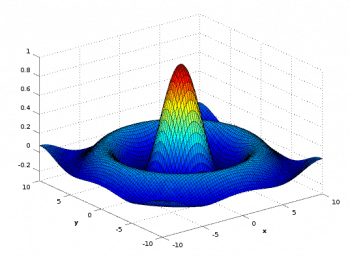
GNU Octave is another important mathematical tool primarily used for numerical computations. It is part of the GNU Project and is offered as free and open source software licensed under the GNU General Public License. GNU Octave is one of the two very powerful open source alternatives to MATLAB, the other being Scilab. But GNU Octave gives far more importance to syntactic compatibility with MATLAB than Scilab does. To prove our point, we have copied and executed the following MATLAB code from the Wikipedia article on MATLAB, on both Scilab and GNU Octave.
<span style="color: #000000;">[X,Y] = meshgrid(-10:0.25:10,-10:0.25:10);</span>
<span style="color: #000000;">f = sinc(sqrt((X/pi).^2+(Y/pi).^2));</span>
<span style="color: #000000;">surf(X,Y,f);</span>
<span style="color: #000000;">axis([-10 10 -10 10 -0.3 1])</span>
<span style="color: #000000;">xlabel(‘{\bfx}’)</span>
<span style="color: #000000;">ylabel(‘{\bfy}’)</span>
<span style="color: #000000;">zlabel(‘{\bfsinc} ({\bfR})’)</span>
Scilab failed to produce an output whereas GNU Octave successfully executed the program. The output obtained from GNU Octave is the same as the output obtained from MATLAB. The output is shown in Figure 3, and you can compare it with the figure given in the Wikipedia article on MATLAB to fully comprehend the syntactic similarity of GNU Octave and MATLAB. GNU Octave can also be used as a programming environment and an interactive shell.
Maxima
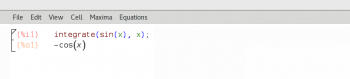
Maxima is a computer algebra system that is widely used in the fields of mathematics like algebra, calculus, etc. Maxima is developed using Lisp, and it is a cross-platform tool that runs on UNIX, Linux, Windows, Android, MacOS, etc. It is free and open source software licensed under the GNU General Public License. Due to the complexity involved in developing computer algebra systems, there are only a few powerful tools like Maxima and SageMath. A very popular graphical user interface (GUI) for Maxima is called wxMaxima, and it can be used as a programming environment and an interactive shell. Figure 4 shows how Maxima can be used to perform integration. I have used a simple function to perform integration, but you can also find the integral of complex functions using Maxima.
SageMath
SageMath is a computer algebra system that has widespread use in various fields of mathematics like algebra, combinatorics, graph theory, numerical analysis, number theory, calculus, statistics, etc. Computer algebra systems are mostly used for symbolic computing, rather than numeric computing and number crunching. The large number of packages necessary for a powerful computer algebra system makes them very rare and due to this reason, SageMath is a very important tool. It is a free and open source tool licensed under GNU General Public License, and is a competitor to many other mathematical tools like Maple, Mathematicia, MATLAB, etc, which are proprietary software. SageMath is not only competent enough to replace any of these tools but also absolutely free. It can be used in two modes, as a programming environment and an interactive shell. The browser-based interactive shell called Notebook has the ability to remember previous inputs and outputs for review and reuse. SageMath is a relatively new tool with most of the development being done using Python; the initial release came out in 2005. Figure 5 shows the logo of SageMath.

R
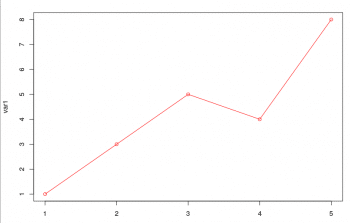
R is a mathematical tool mainly used for statistical computing. It is used by mathematicians in general and by statisticians in particular for data mining and developing statistical software. The development of R is supervised by the R Foundation for Statistical Computing. R is a cross-platform tool that can be used in various operating systems like Linux, Microsoft Windows, etc. R is free and open source software licensed under the GNU General Public License. It is often used as an open source alternative to proprietary statistical packages like SAS, SPSS, etc. But R being freely available is not the main reason for its widespread adoption by the statistical community; rather, its popularity is based on its power. R can be used as a command line utility as well as with a graphical user interface (GUI). A very popular GUI for R is called the RStudio. R is also capable of performing various graphical techniques. Figure 6 shows the output of the simple R commands ‘var1 <- c(1, 3, 5, 4, 8)’ and ‘plot(var1, type=”o”, col=”red”)’ when executed on the console.
Isabelle
While choosing ten useful mathematical tools for this article, we made sure that what we selected is used in diverse fields of mathematics, rather than choosing ten popular software from a single field, like numerical computations, for instance. So, this tool may not be as popular as many other mathematical this tools left out from this list. Let us clarify further—the general public is familiar with numerical computing tools like MATLAB, Scilab, etc, but may not be aware of SageMath or Maxima because the latter two are mostly used in the more abstract areas of mathematics like combinatorics, graph theory, number theory, etc. Mathematics itself is often considered an abstract subject – sometimes even by famous mathematicians. G.H. Hardy once said, “We have concluded that the trivial mathematics is, on the whole, useful, and that the real mathematics, on the whole, is not.” There are certain fields in mathematics which are deemed abstract even by the standards of professional mathematicians; one such field is logic and automatic theorem-proving. Not many people are interested in automatic-theorem proving, but for the select few who work in this area, a tool to aid their quest will be like a gift from heaven. So, with that rationale, we introduce Isabelle, an interactive theorem-proving software. It is free, open source and available for use under the BSD licence. Isabelle has been developed by using two programming languages, ML and Scala. It can be used to encode first-order logic, higher-order logic, etc, for further processing. Figure 7 shows the logo of Isabelle.
SciPy
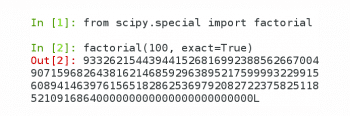
SciPy is an open source Python library used for scientific computing. It contains modules for optimisation, linear algebra, calculus, interpolation, Fast Fourier Transforms, signal processing, image processing, etc. SciPy is part of the NumPy stack, which also includes tools like Matplotlib, SymPy, etc. Matplotlib is a plotting library and SymPy is a library for symbolic computing in Python. The SciPy library is available under the BSD licence. Figure 8 shows how SciPy is used to find the factorial of 100. Even in a modest computer system, we were able to find the factorial of 100,000. But we will not dare to show the output in this article because the resulting number is 456574 digits long. The December 2017 issue of OSFY had 108 pages, including the covers. The page we randomly chose in that issue had 54 lines of text and the line we randomly chose had 123 characters, so, a simple calculation will tell you that it will take at least 68 pages of the next issue of OSFY to print this number. This tells us about the power of SciPy. And with a powerful computer, you could do wonders with SciPy.
gnuplot
Scientific research involves representing data in a neat and concise manner. Graphs are often used to do this. It’s for this purpose that we can use gnuplot, a command line program that can plot 2D and 3D graphs of functions and data. It is frequently used in vector graphics. gnuplot can produce output in many different image formats like Portable Network Graphics (PNG), Encapsulated PostScript (EPS), Scalable Vector Graphics (SVG), Joint Photographic Experts Group (JPEG), etc. It is a cross-platform utility that runs on a variety of operating systems like UNIX, Linux, Microsoft Windows, MacOS, etc. Even though the name of the software starts with ‘gnu’, it is not part of the GNU project. In fact, the inclusion of gnuplot in this list can be contested because, in a very strict sense, it is not free and open source software because it is licensed under the gnuplot licence, which gives users the right to modify the source code but the right to distribute modified versions is withheld. But the extreme popularity of gnuplot made us select it rather than a free and open source graph plotting utility like xgraph. Figure 9 shows a 3D graph plotted using gnuplot.
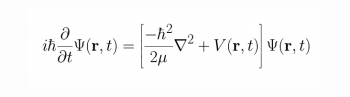
LaTeX
Finally, let us think about the life of a brilliant mathematician who has done a lot of research –with and without using some of the mathematical tools we have listed just now—to come up with some excellent theorems. It’s eventually time to write down these results to bring out a good scientific paper. Do remember that mathematics is full of symbols like π, √, ∞, etc, which are normally not available on the keyboard. Preparing scientific papers in the required format of various scientific journals is a very tedious task due to reasons like this. So, every mathematician will eventually use a document preparation system and the best one is LaTeX. It is widely used in academia and the industry, to prepare scientific documents in areas like mathematics, statistics, computer science, engineering, etc. LaTeX is cross-platform, free and open source software licensed under the LaTeX Project Public License. It can also be used for efficient reference management. Figure 10 shows the time-dependent Schrödinger equation rendered using LaTeX.
Before concluding the article, we need to make a confession —like all Top Ten lists, this too is coloured by personal preferences and prejudices. But we have tried to make the list as diverse and useful as possible so that not just students and practitioners of mathematics, but professionals in computer science, physics, chemistry, etc, can also appreciate and use these tools to their advantage.