This article looks at how DTMF technology has evolved over the years, and can still be of use.
In the days of analogue telephone communication, the most common type of cable that was used for connectivity was the unshielded twisted pair (UTP). Since it did not have a physical shield to block any interference, the amount of interference was a bit high. However, it was not too noisy and was good enough to transmit voice. But as the days passed and the number of people using telephones increased, the need for an automated telephone exchange increased too. It was in January 1958 that G. Goertzel published a paper called ‘An Algorithm for the Evaluation of Finite Trigonometric Series’, in the American Mathematical Monthly. This became the basis of dual tone multiple frequency (DTMF) signalling. It allowed us to encode numeric values as superpositions of two co-prime sine waves in such a way that they became noise-resistant.
On November 18, 1963, Bell Systems introduced phones with buttons instead of rotary dials. DTMF assigned a special tone to each button pressed on the telephone device. As a number was dialled, each button that was pressed gave a standard audio signal. The telephone exchange could decode these signals as DTMF to find out what number the user had typed in.
Binary was defined by ‘on’ and ‘off’ or ‘1’ and ‘0’. DTMF technology worked by having the handset generate tones at specific frequencies and playing them over the phone line when a button was pressed on the keypad. It could be treated like a device to switch up to eight appliances. Equipment at the other end of the phone line listened to the specific sounds and decoded them into commands.
The Goertzel algorithm is a digital signal processing (DSP) method for quickly evaluating each discrete Fourier transform term (DFT). It is beneficial in some real-world situations, such as when recognising the DTMF tones emitted by the pushbuttons on a classic analogue telephone’s keypad. The spectral data can be quickly and efficiently extracted from an input signal using this approach. In order to efficiently compute DFT values, it essentially makes use of two-pole IIR type filters. As a result, it is a recursive structure that always processes one incoming sample at a time, as opposed to the DFT (or FFT), which must first have a block of data to begin processing.
Now, let’s break this down into several simple steps.
A DTMF signal consists of two sine waves, one chosen from one of four low-frequency tones, and one chosen from one of four high-frequency tones, where we are mapping each number to a tuple of its coprime frequencies, as shown in Table 1. The table shows how digits can be converted to frequency ranges, of which the upper and lower bounds are given.
| Digits | Upper bound | Lower bound |
| 1 | 1209 | 697 |
| 2 | 1336 | 697 |
| 3 | 1477 | 697 |
| 4 | 1209 | 770 |
| 5 | 1336 | 770 |
| 6 | 1477 | 770 |
| 7 | 1209 | 852 |
| 8 | 1336 | 852 |
| 9 | 1477 | 852 |
| * | 1209 | 941 |
| 0 | 1336 | 941 |
| # | 1477 | 941 |
For example, when you press the button ‘1’ on a phone keypad, a signal consisting of a sine wave at 697Hz plus one at 1209Hz is generated. To fiddle around with DTMF and its encoding and decoding, we have written a library. The library has the functions dtmf_encoder() to convert the input number to its corresponding DTMF audio, and decode_dtmf() to decode the same.
Okay, now let us try to encode a number like 76589410. We simply write the command:
tone_2 = dtmf_encoder(‘76589410’) IPython.display. Audio (tone_2, rate = Fs)
In the above command, we are converting each digit into DTMF audio signals by taking sine waves at the required frequencies.
For convenience, plotting the graph of such audio signals taking the sampling rate Fs = 24000Hz is shown in Figure 1.
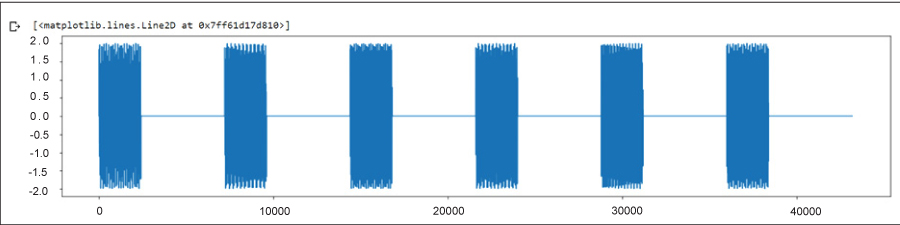
It is clearly visible from the plot that each number is a superposition of two different sine waves at two different frequencies.
Now let’s encode a number and special character series of 1498*0:
tone_1 = dtmf_encoder(‘1498*0’) IPython.display. Audio (tone_1, rate = Fs)
The above command will also display the audio representations of the frequencies with a customisable speed. We can see their size and represent this in a graphical form, as shown in Figure 2.
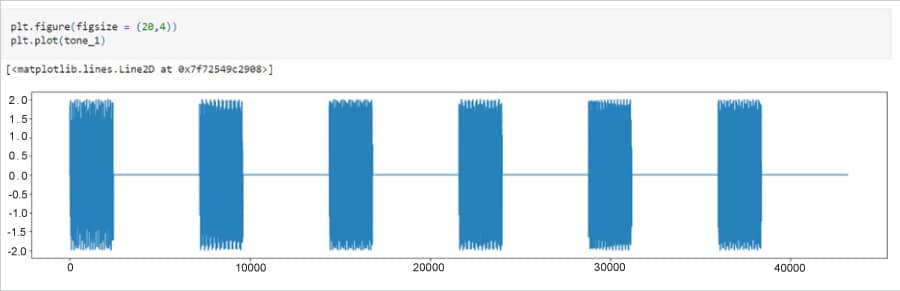
Similarly, we may also decode the DTMF frequencies into required digits as before using a simple algorithm where we try to dissect the numbers according to the frequency ranges they represent. We check the upper bound and lower bound of the frequencies by converting it into NumPy arrays. For example, to decode ‘1498’ we get a frequency between 697Hz to 1209Hz, so we know that the first digit is one. The next one lies between 770Hz to 1209Hz, and so on.
Hence, we execute the decoding code in the dtmf_decode() function by calling the functions given below:
print(decode_dtmf (tone_2)) # works perfectly!! [‘7’, ‘6’, ‘5’, ‘8’, ‘9’, ‘4’, ‘1’, ‘0’] print(decode_dtmf(tone_1)) [‘1’, ‘4’, ‘9’, ‘8’, ‘*’, ‘0’]
Now, we can see how tone_1 and tone_2, which were an overlapping sinusoidal wave of frequency ‘2’, are being converted to the original sequence with minimal error.
Figure 3 shows the energy graph of DTMF frequency transformation.
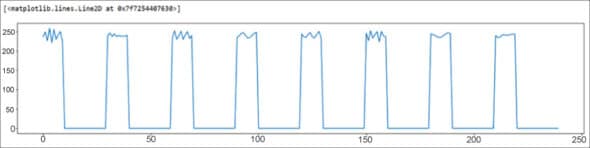
DTMF is used even today. Often, when dialling a customer care number, we are greeted with the automated response of ‘For English, press 1, for Hindi press 2’, and so on. This selection menu on voice calls would have been a challenge were it not for DTMF. The key that the user taps for a particular selection is encoded as DTMF and then decoded at the receiver’s end to get the user’s choice.
However, the use of DTMF was not as simple as it seems. It was vulnerable to an attack called ‘phreaking’. This attack used a malicious actor to send unauthorised DTMF signals by hooking up some custom hardware on the telephone lines. In some regions of the United States, it is illegal to connect anything to the telephone line for the same reason.
A lot of applications and systems can be built using the concepts explained in this article. So this retro technology is evergreen!




