After Google’s dramatic announcement of quantum supremacy, quantum computing has caught the public eye and has generated enormous interest in the subject. Leap, the real-time quantum application environment, even provides one minute of free quantum computing time. This article discusses some aspects of quantum computing from the layman’s perspective.
In 2019, Google claimed quantum supremacy and that generated a lot of interest about quantum computing among the general public. But are we on the verge of developing quantum computers that can revolutionise the world? Experts differ on this matter with many claiming quantum computers will be a reality in the very near future, whereas some others (though in the minority) take the extreme opposite view that quantum computers will never be a reality. Whatever might be the eventual outcome, quantum computing is an exciting technology and will remain in the public eye for quite some time.
The quantum computing vocabulary
Let us begin by discussing the two terms that are often associated with quantum computing — quantum superposition and quantum entanglement. I don’t have the expertise or audacity to try to explain the above two concepts. Moreover, it takes a lot more than a short article to explain these. But let us, at least, go through the definitions of these two quantum mechanical phenomena to understand why a quantum computer is far more powerful than a classical computer (the computers we use today). According to Wikipedia, a quantum state is a mathematical entity that provides a probability distribution for the outcomes of each possible measurement on a system.
Quantum entanglement is the phenomenon by which the quantum states of a pair of particles are interdependent, irrespective of their physical proximity. Quantum superposition is the phenomenon by which a quantum system can be in a combination of several separate quantum states at the same time. Notice that the above two definitions are not rigorous enough to capture the full intricacies of these quantum mechanical phenomena. A quantum computer is a device that uses these quantum mechanical phenomena to perform computations. In quantum computers we have qubits (quantum bits) for data storage in place of bits used in the classical computers of today.
The quantum mechanical phenomenon described earlier called superposition makes qubits far more powerful than classical bits, which in turn makes quantum computers far superior to classical computers. What makes a qubit more powerful than a bit in a classical computer? In a traditional bit, we can store either a 0 or a 1. The corresponding basis values stored in qubits are represented by |0> and |1>. The power of a qubit comes from the fact that it can store a combination of the basis states of |0> and |1>, in addition to the basis states themselves, due to quantum superposition. Notice that a classical bit will be in either of the two states of 0 and 1, whereas the qubit can also be in a superimposed state of |0> and |1> and not just any one of them. The difficulty in manufacturing quantum computers arises from the fact that in order to make qubits, we need objects that can attain a state of quantum superposition between two states.
There are different ways to create a system capable of exhibiting quantum superposition. Some of the techniques involve suspending ions in vacuum by using an electromagnetic field, positioning single atoms in crystals, using photons in optical fibres, etc. But all these techniques are difficult to implement, especially when the number of qubits in a system increases. This makes the creation of quantum computers extremely difficult. Another term often associated with quantum computing is quantum supremacy. It is a term defined by John Preskill, a theoretical physicist, and it denotes the ability of a quantum computer to get a solution to a problem for which no solution is feasible by a classical computer. For example, for a classical computer it is extremely difficult to find the factors of a large semiprime (a number that is a multiple of two prime numbers). If the number is sufficiently large, even the fastest supercomputer in the world will take thousands of years to find the factors of semiprimes (this is what makes public key cryptography effective). A quantum algorithm called Shor’s algorithm can solve this problem of integer factorisation in polynomial time, making it a feasible solution.

So a quantum computer can solve the problem of integer factorisation in minutes or even seconds, instead of the thousands of years required by even the fastest classical computer of today. Quantum cryptography is yet another term often associated with quantum computing. It involves the use of quantum mechanical properties for cryptographic purposes. Strictly speaking, quantum cryptography has an existence that is independent of quantum computing. Notice that post-quantum cryptography (the study of cryptographic techniques that will be able to withstand the attack of quantum computers) is distinct from quantum cryptography. For example, in a world where quantum computers are common, public key cryptography as we know today will not be secure enough to be used in sensitive fields like banking, commerce, etc.
The power of quantum computers
With the necessary vocabulary about quantum computing built, let us now discuss the potential power of quantum computers, if and when they are ready and deployed. In what ways are they superior to classical computers? Consider a classical computer with N bits of storage. It can store a single number between 0 and 2N-1 in binary. Now consider a quantum computer with N qubits of storage. Any number between 0 and 2N-1 can be stored in this qubit storage but with a certain probability for the presence of each number.
At this stage, I would like to point out a misconception about the way qubits work. People often believe that we can store all the numbers between 0 and 2N-1 in N qubits — all at the same time. This is not the case. What we can say is that multiple readings of the N qubits in a quantum computer may yield different numbers, and the power of quantum computing comes from this fact. To further elaborate the additional power we can extract from a quantum computer, let us try to understand complexity classes.
A computational problem is said to be in complexity class P, if it can be solved by a classical computer in polynomial time. Let us say that if a computational problem is in class P, then we can solve the problem in a reasonable amount of time even if the problem input is sufficiently large, by using a classical computer. Examples for problems in class P include addition, subtraction, multiplication and division of numbers, sorting a list of numbers, searching for a number in a list, checking whether a graph contains an Eulerian cycle, etc. In general, we can say that problems in class P have a feasible solution. There are many other complexity classes also, all of which in some sense tell us how difficult it is to obtain a solution to a computational problem. For example, there are no known polynomial time (feasible) solutions to problems in class NP. Examples for problems in class NP include the Hamiltonian cycle problem, travelling salesman problem, clique problem, subset sum problem, etc. It is not known whether polynomial time solutions to these problems exist. In fact, the P=NP problem is one of the most important open problems in computer science. You could win a million dollars by solving it!
Having given the necessary introductions about complexity classes, let me dispel another myth about the power of quantum computers. People often incorrectly assume that a quantum computer will be able to solve all the problems in class NP in polynomial time. This is not what the experts believe.
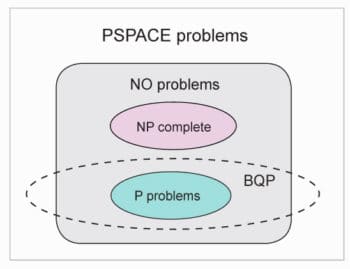
Figure 1 shows a probable Venn diagram of some of the complexity classes, including the quantum complexity class BQP (Bounded-error Quantum Polynomial time). It is the class of problems that can be solved by a quantum computer in polynomial time with an error probability of at most 1/3. From Figure 1, we can have an idea about the kind of problems that can be solved efficiently by a quantum computer. It will definitely outperform any classical computer but, at the same time, the wide consensus among experts is that at least some of the problems in class NP will not be solvable by a quantum computer in polynomial time.
Now let us consider undecidable problems. These problems (could be thought of as unsolvable problems, though this is not a mathematically precise definition) are decision problems (the answer to such problems is either ‘yes’ or ‘no’) for which no algorithm exists to help us get an answer. An example is the Post correspondence problem. No classical computer can solve this problem algorithmically. What about quantum computers? Sadly, the problem remains unsolvable even if we use a quantum computer. So an important observation about quantum computers is the following. As far as ‘computability’ is considered, quantum computers do not have any advantage over classical computers. If a problem is undecidable (unsolvable) by a classical computer, it remains the same for quantum computers. At the same time, quantum computers will efficiently solve a lot of problems not feasible for classical computers.
The progress made so far
Now that we know about the extra power that will be provided by fully functional quantum computers, let us discuss the different companies and research institutes that have made significant advances in quantum computing. As it can be a game changing technology, all the tech giants have invested heavily in quantum computing. Big players like Google, IBM, Microsoft, HP, Intel, Toshiba, etc, all have their own divisions to carry out research on quantum computing. Each one of these companies has contributed either to the hardware or the software for quantum computing.
In 2016, MIT (Massachusetts Institute of Technology) and the University of Innsbruck, Austria, together developed the first functional quantum computer. Though that quantum computer could only factorise relatively small numbers like 15 using Shor’s algorithm, it was a tremendous achievement as far as quantum computing was concerned. The next big milestone came in 2019. Google claimed quantum supremacy in October 2019. The tech giant developed a 53 qubit quantum processor called Sycamore, which it claimed achieved quantum supremacy by completing a computational task in 200 seconds. That computation would have taken at least 10,000 years for even the fastest classical supercomputer we have today, claimed Google. The report about the experiment, published in the famous journal Nature, can be found at https://www.nature.com/articles/s41586-019-1666-5#Abs1. Figure 2 shows Google’s Sycamore quantum processor mounted on a cryostat.
Though the news of such a quantum processor made quite a sensation in the media, the claim of achieving quantum supremacy was questioned by many. IBM claimed that the same task could be completed in under 2.5 days in a classical computer. The company also claimed that further improvements might reduce the time taken for the solution even further. Details regarding the claims made by IBM can be found at https://www.ibm.com/blogs/research/2019/10/on-quantum-supremacy/. IBM has also touched significant milestones as far as quantum computing is concerned. It has already developed tools like Qiskit (an open source SDK for working with quantum computers) and Quantum Lab (allows online code development for quantum circuits), which are available to the programming community for testing and development. Another big player in the field of quantum computing is Microsoft. Quantum Development Kit (QDK) and Q# (Q Sharp, a quantum programming language) are some of the important contributions made by Microsoft to quantum computing.
Quantum computer simulators
Now that we have seen the contributions from different companies and organisations to quantum computing, let us discuss quantum computer simulators. We have seen that developing quantum computers is an extremely difficult task. So, how can researchers test a new quantum algorithm? Quantum simulators help us achieve this by using classical computer hardware to imitate quantum behaviour. The difficulty in simulating quantum behaviour arises from the exponential time requirement by classical computers — as the number of qubits increases, the simulation becomes slower and slower. QuEST, developed by the University of Oxford, is an example of quantum computer simulators.
The development of these simulators has also led to the recent popularisation of quantum clouds, a platform that is trending nowadays. Yes, it is true! I have seen quite a number of advertisements offering free quantum cloud time and if entrepreneurs are pouring in their resources, there ought to be some truth behind these. Some of these quantum computer simulators are based on the quantum annealing technique. I believe that in the near future a lot of startups will come up with brilliant ideas to offer more and more quantum cloud resources. An example of quantum cloud services is the IBM Quantum Experience. It allows users to graphically build quantum circuits and develop quantum programs using Qiskit, an open source quantum software development kit (see Figure 3).
Quantum programming languages
Any general discussion on quantum computers will be incomplete if we do not discuss quantum programming languages. What are the important quantum programming languages? We have already mentioned Q# (Q Sharp), a quantum programming language developed by Microsoft. It is a free and open source programming language licensed under the MIT License. This programming language allows us to use qubits in algorithms. The syntax of Q# is related to the syntax of C#, a classical programming language, also developed by Microsoft. Q# is a high-level programming language, whereas OpenQASM is an assembly language used for quantum programming. An implementation of OpenQASM is used with the IBM Quantum Experience quantum cloud computing platform. It is a free and open source programming language licensed under the Apache License. Cirq is a framework for Noisy Intermediate Scale Quantum (NISQ) computers, developed by Google. This is also free and open source software licensed under the Apache License. Cirq uses the Python programming language for developing quantum algorithms. There are a lot of other quantum programming languages, but the support by Microsoft, IBM and Google makes the above mentioned languages significant.
The role of open source
Before we wind up our discussion, it is essential to answer an important question. What is the role played by the open source community in quantum computing? Of course, quantum computing is a field where you need a gigantic budget for hardware research. But, what about the programming community? There might be a day when there are millions of quantum computers in the world, just like the classical computers we have today. The best news for the open source community is that almost every software related to quantum computing is open source. We have already seen examples of quantum programming languages, and almost all of them are free and open source. The same goes for other quantum computing resources also. Being a new technology, it is essential to have the support of a large community. I believe the developers of quantum computing feel that the open source model is the best to sustain and nurture such a developing technology. Let us hope that the year 2020 for quantum computing will be the same as the year 1950 was for classical computing. We only had two digital computers, UNIVAC and EDSAC, in 1950. Look at the computing power we have today. Hopefully, we will witness a similar revolution in quantum computing in the near future.