It is election time in India and the whole country is watching the latest election news, discussing the functioning of EVMs and the code these use, and talking about which party will form the new government. The author takes this opportunity to explore a different kind of electoral system, in which votes are given to candidates in order of preference. We explore the code in such a situation, and look at how the winner is determined.
Intuitively, we understand that an election’s outcome will be affected by the nature of the process. Many countries use a run-off between the top two candidates, and the leader of the first round may not make it through the second round. There is also the possibility of an instant run-off in which everyone votes for multiple candidates in the order of preference. Given the time and effort involved in the Indian elections, the instant run-off would seem to be an attractive alternative. However, it is fun to see if we can simulate outcomes by modelling an election. Let us model an instant run-off election with only a second preference vote. The application we will use is NetLogo, which is ‘a multi-agent programmable modelling environment’.
You can get started with NetLogo at http://ccl.northwestern.edu/netlogo/.
NetLogo is based on the concept of patches. We will assume that each patch represents a constituency. Each constituency will have N candidates, the number of which will vary at runtime. Each tick will represent a voter voting.
Each voter will vote twice. The first vote will be for any one candidate, and the second one for any other candidate.
For the sake of simplicity, voting will be random. However, we will configure the preferred candidates, who will have double the chance of getting a vote.
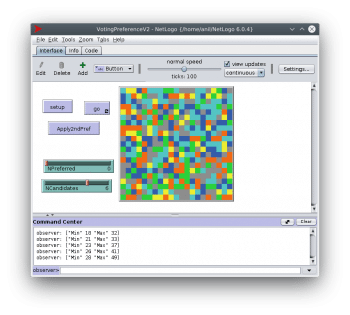
Figure 1 displays the interface for this model. The Setup button initialises the model. The Go button counts the votes and shows the results based on the first preference votes. The button for processing the second preference votes will display the result (after the second preference votes have been processed).
The data structures
Keeping track of first preference votes is easy. For each constituency, we need an array or a list with a vote count for each candidate. Keeping track of second preference votes is trickier. We need to be able to count them and check if the first preference candidate has been eliminated. Hence, this will need to be a list of lists, in which each list represents the votes cast for a candidate, given that the first preference vote was for a specific candidate.
The setup code
The code is written on the ‘Code’ tab. If you remember Logo from your school days, you can get a feel for the programming style. The coding style is heavily oriented towards functional list processing paradigms. If you have programmed in Python, you will need to keep looking at the syntax but programming will not be that difficult.
globals [NVoters] patches-own [votes nextPref candidate winner loser listc]
The patches-own are variables that are for each patch, which, in our case, is a constituency. The lists, votes and nextPref keep count of the first and second preference votes. The last two variables, loser and listc, are needed to process the second preference votes of the current loser. The second preference votes are added to the votes of the candidates who have not been eliminated.
to setup clear-all set NVoters 100 let initListOfList [] repeat NCandidates [ ; add a list of N 0’s as the last element of the list set initListOfList lput n-values NCandidates [0] initListOfList ] ask patches [ set votes n-values NCandidates [0] set nextPref initListOfList ; create a list [0 1 ... N-1] set listc range NCandidates ] reset-ticks end
The Main Code
In the interface, the Go button will have ‘Forever’ ticked.
to go vote tick if ticks = NVoters [ compute stop ] end
The vote procedure is now called. Every tick increments the counter. The loop stops when each voter has voted and the result computed.
to vote ask patches [ ; the first NPreferred candidates get double the chance set candidate random (NCandidates + NPreferred) mod NCandidates ; increment the vote count of the candidate set votes replace-item candidate votes ( item candidate votes + 1 ) ; change the colour of the patch to the current candidate set pcolor 20 * candidate + 5 second_pref_vote ] end to second_pref_vote ; select the list for for first preference candidate let votes2 item candidate nextPref ; each remaining candidate gets the same chance let pref2 random (NCandidates - 1) if pref2 >= candidate [ set pref2 pref2 + 1 ] ; increment the vote count and update the list of lists set votes2 replace-item pref2 votes2 ( item pref2 votes2 + 1 ) set nextPref replace-item candidate nextPref votes2 end
The ‘ask patches’ loops over each patch/constituency.
The methods given above just take a random vote and store the result in suitable lists.
to compute let vmin NVoters let vmax 0 ask patches [ ; index and candidate are the same for the first pref vote ; but as candidates are eliminated, the two will not be the same. let idx position max votes votes set winner item idx listc set vmax max list vmax max votes set vmin min list vmin max votes set pcolor 20 * winner + 5 ] show (list “Min” vmin “Max” vmax) end
In addition to finding the candidate with the maximum votes, the method also finds the maximum and minimum votes of the winning candidates.
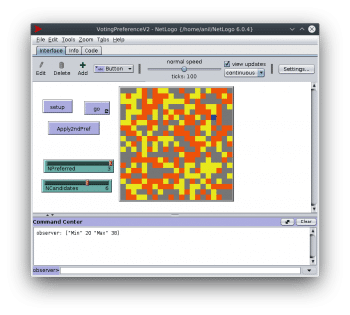
Figure 2 shows the results with only the first preference votes.
Processing for the second preference
The losing candidates are eliminated, and their votes are transferred to the remaining candidates. The process is repeated until only two candidates are left.
to process repeat NCandidates - 2 [ apply_nextPref compute ] end
The hard part is handling the votes for candidates who have been eliminated. In the first preference votes, the item in the list itself is removed. In the second preference votes, it is simpler to mark eliminated candidates’ votes by the place holder -1.
to apply_nextPref ask patches [ ; select the losing candidate set loser position min votes votes ; remove his votes set votes remove-item loser votes ; remove 2nd pref votes remove-loser-nextPref set listc remove-item loser listc ; -1 votes is used for eliminated candidates let votes2 filter [ i -> i != -1 ] item loser nextPref ; transfer 2nd pref votes to the remaining candidates set votes (map + votes votes2) ] end to remove-loser-nextPref ; replace votes of losing candidate by -1 in each list let c item loser listc let tempList [] foreach nextPref [ x -> let v2 replace-item c x -1 set tempList lput v2 templist ] set nextPref tempList end
Figure 3 shows the results after the second preference votes are counted. This is not a serious model, but just to check and demonstrate that the results can be very different if second preference votes are applied.
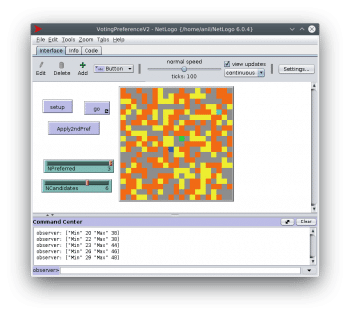
After the second preference votes are applied, the winners will be closer to crossing the 50 per cent mark, though not always, as some second preference votes would have been for the candidates who are eliminated.
The model chosen was very simple so that the ideas of how to model in NetLogo can be explored. Greater complexity can be added, and it is fun to program in a language with syntax different from the procedural languages.
One aspect of NetLogo that we have not used or explored is the use of turtles. Each candidate could be a turtle, belonging to a party or could be an independent. The model can be mind-bogglingly complex. You can go ahead and create one in which your favourite party wins!